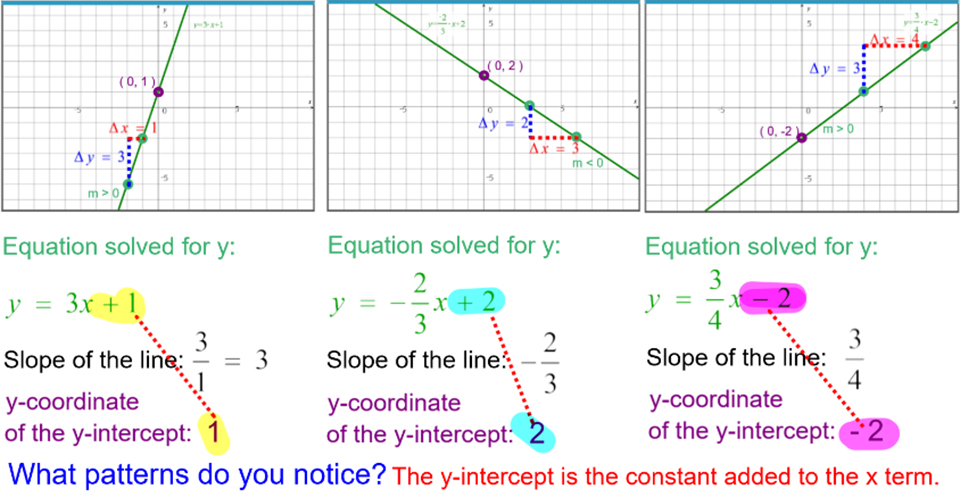
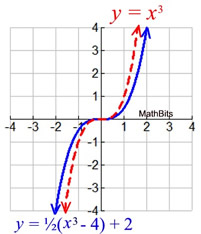
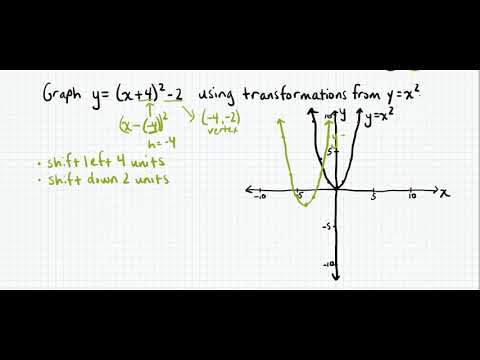
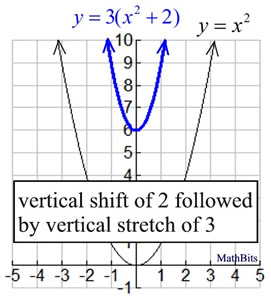
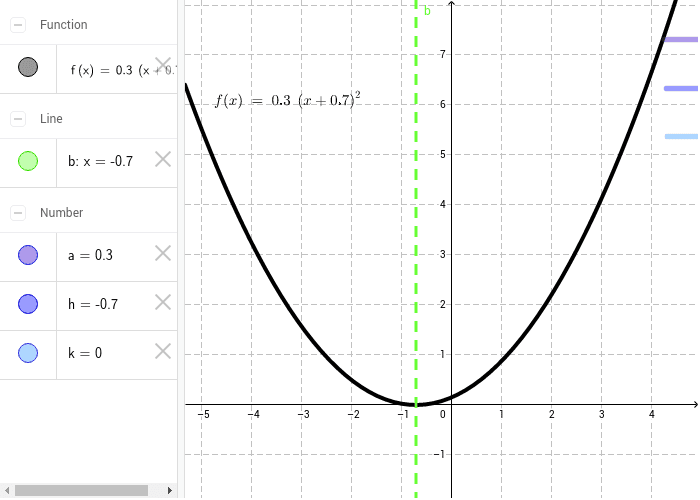
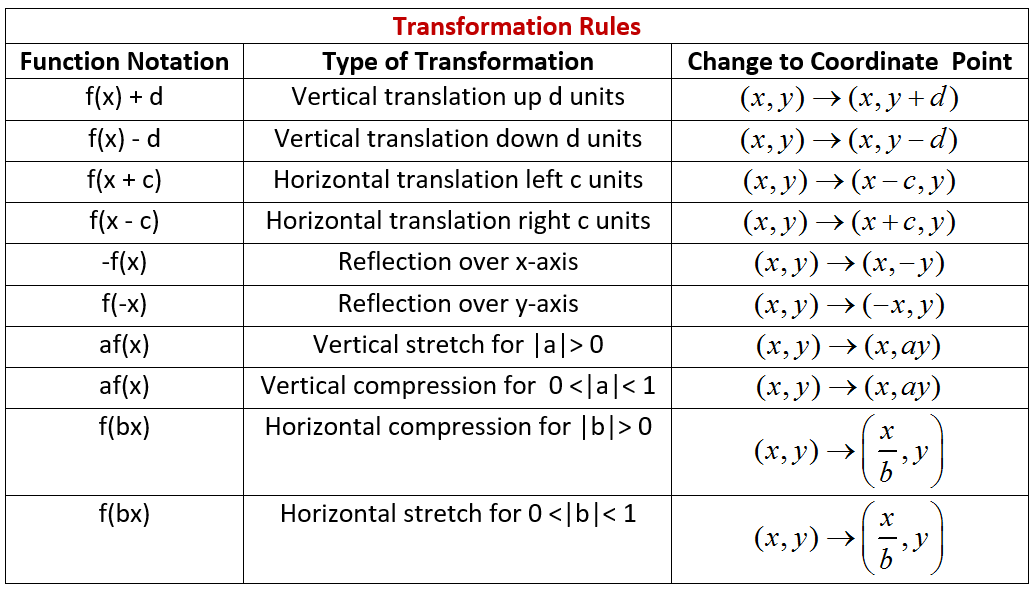
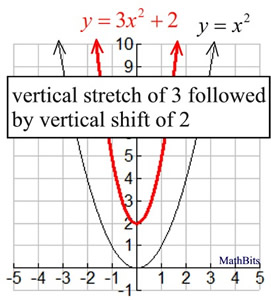
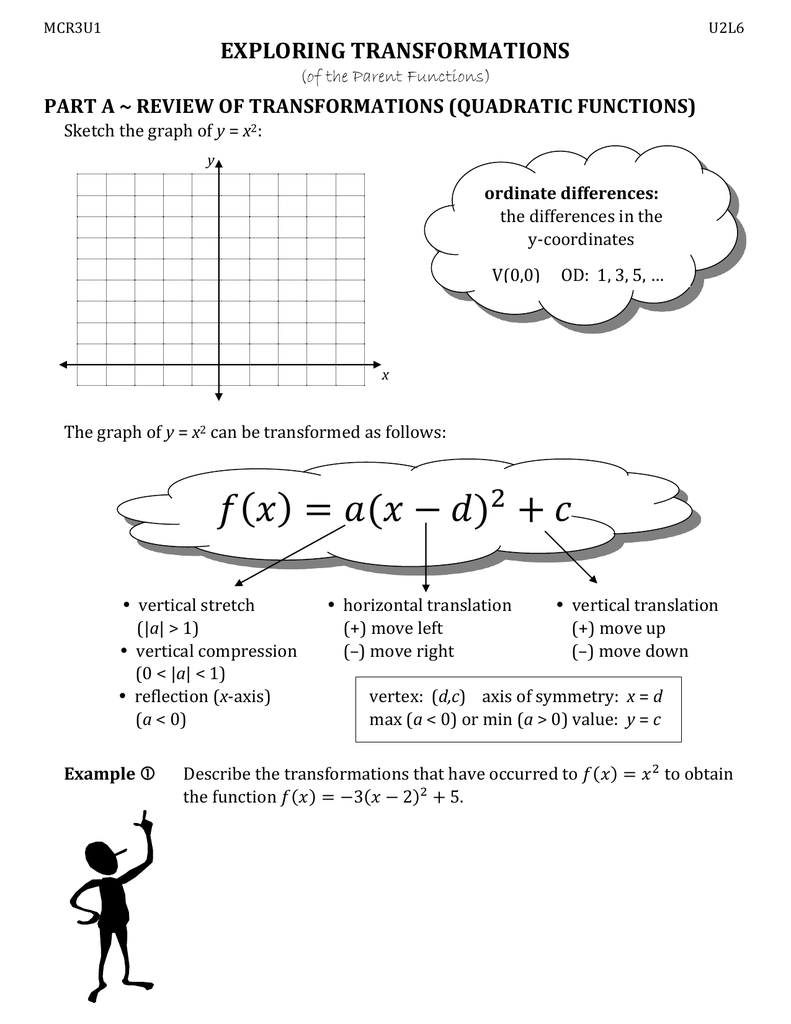
An easy way to remember what happens to the graph when we add a constant add to y to go high add to x to go left We can stretch or compress it in the ydirection by multiplying the whole function by a constant g (x) = 035 (x2) C >
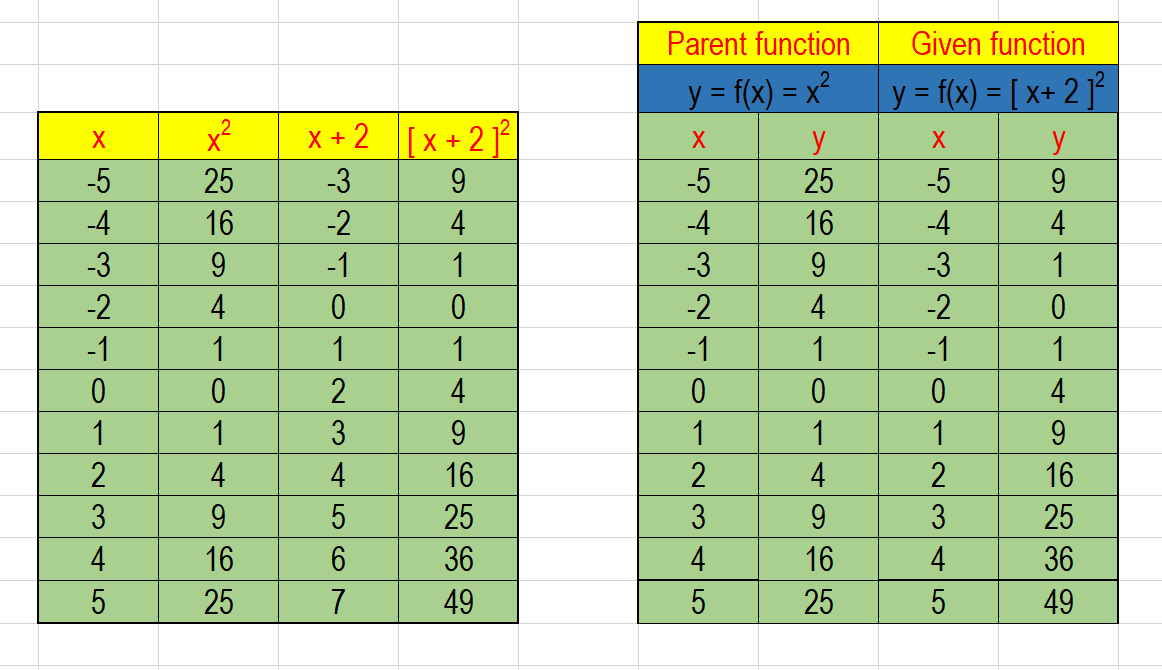
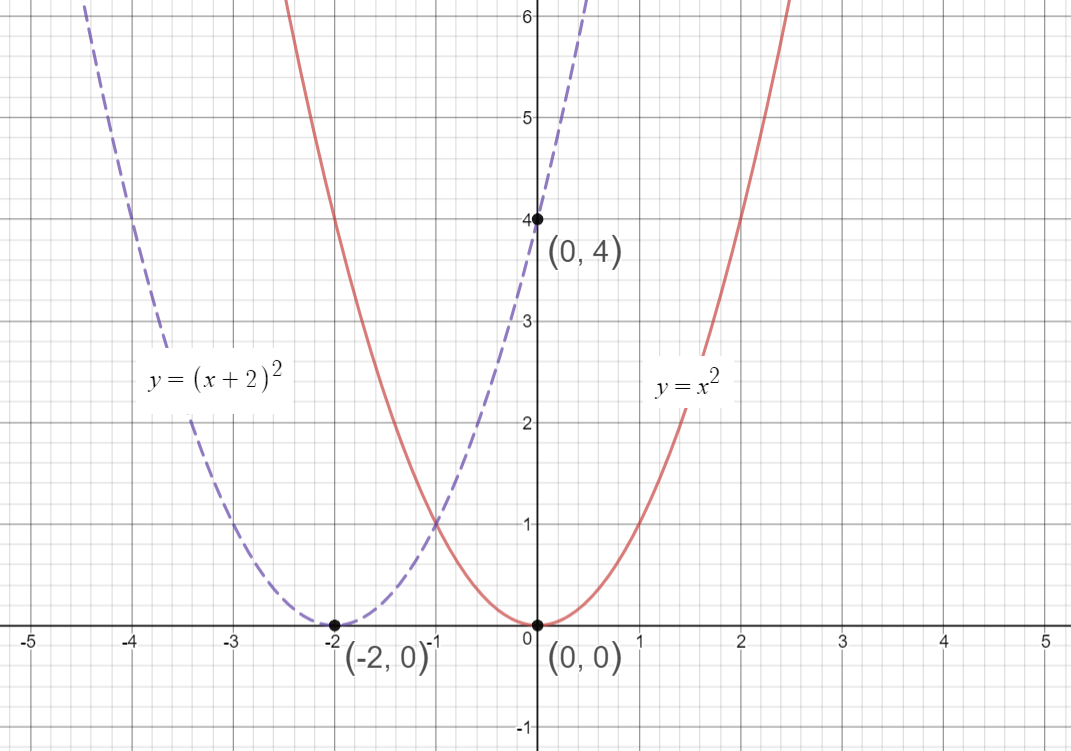
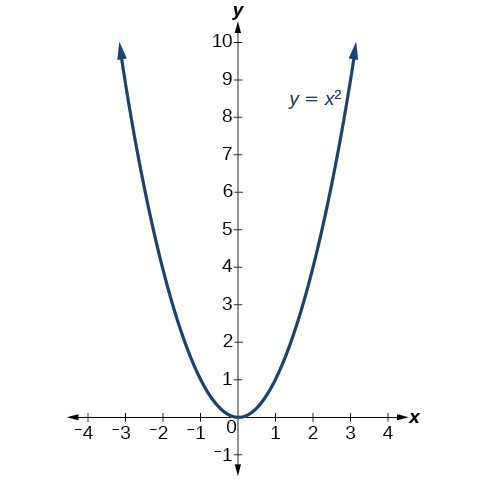
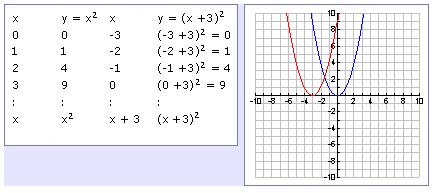
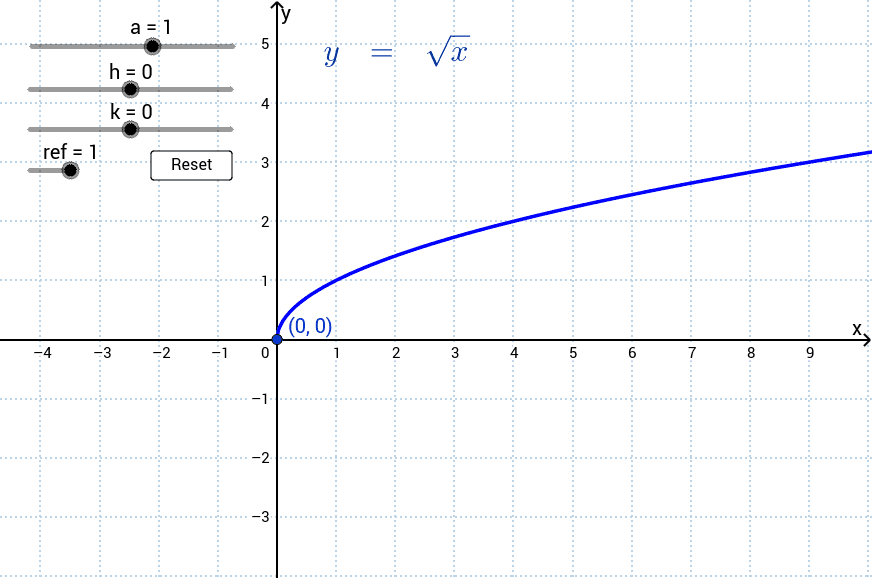
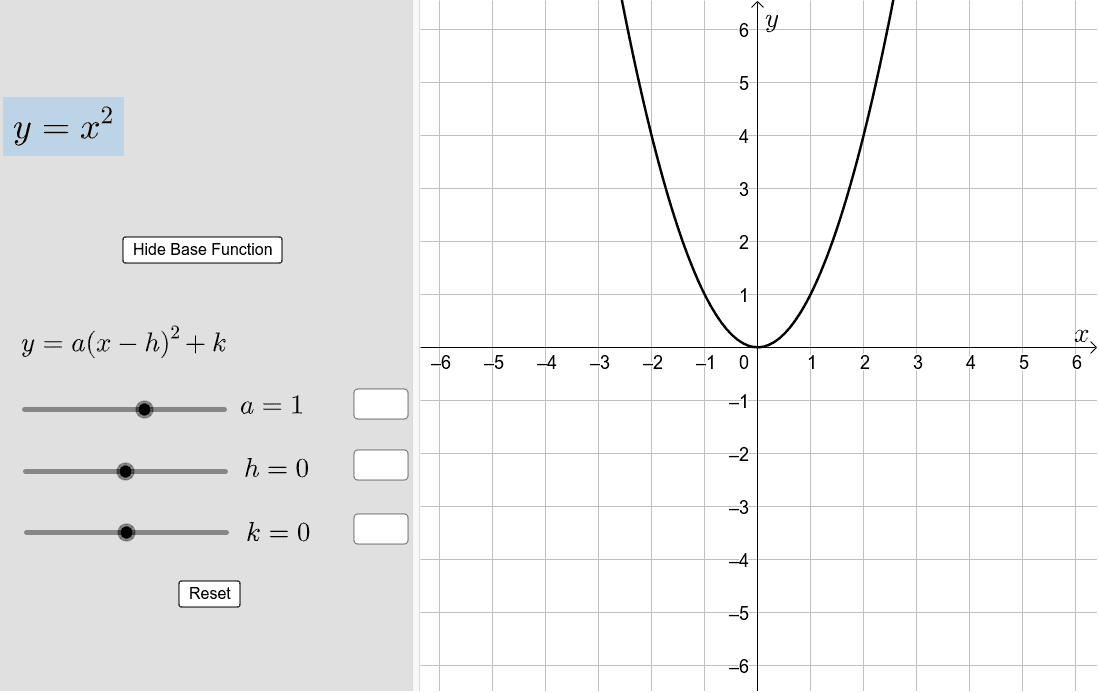
Graph of y=x^2 transformations-The graph of \ (f (x) = x^2\) is the same as the graph of \ (y = x^2\) Writing graphs as functions in the form \ (f (x)\) is useful when applying translations and reflections to graphs(x,y) → (x,y) To rotate 270º
Graph of y=x^2 transformationsのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
 |  |  |
 | ||
「Graph of y=x^2 transformations」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 | 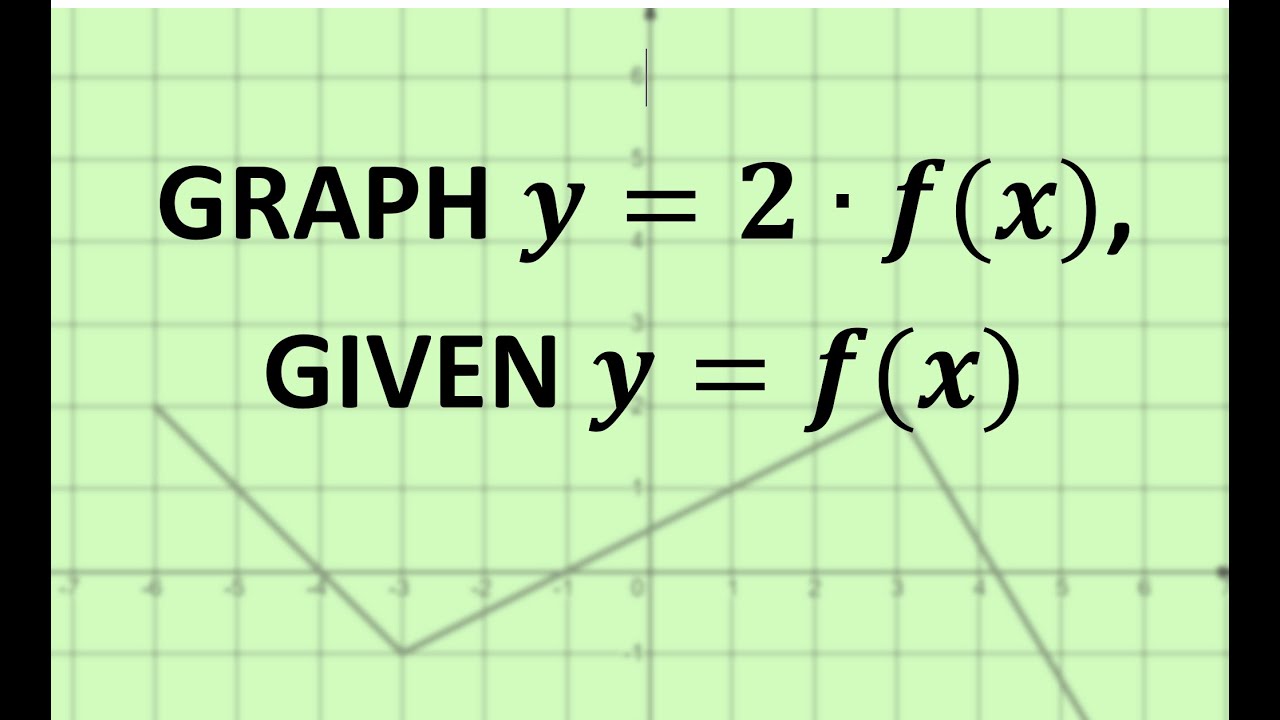 | |
「Graph of y=x^2 transformations」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 | 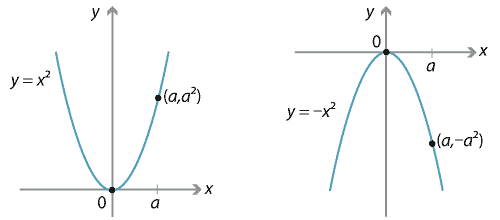 |  |
「Graph of y=x^2 transformations」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  | |
「Graph of y=x^2 transformations」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | 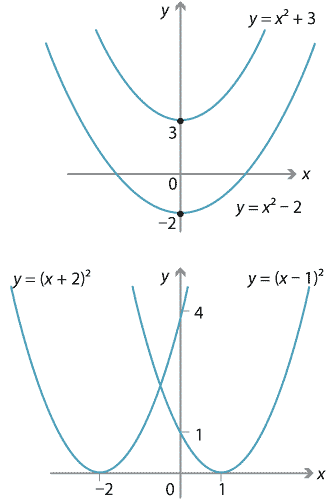 |
 |  |  |
 |  |  |
 |  |  |
「Graph of y=x^2 transformations」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  | |
「Graph of y=x^2 transformations」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  |  |
「Graph of y=x^2 transformations」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 | ||
 |  |  |
「Graph of y=x^2 transformations」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | 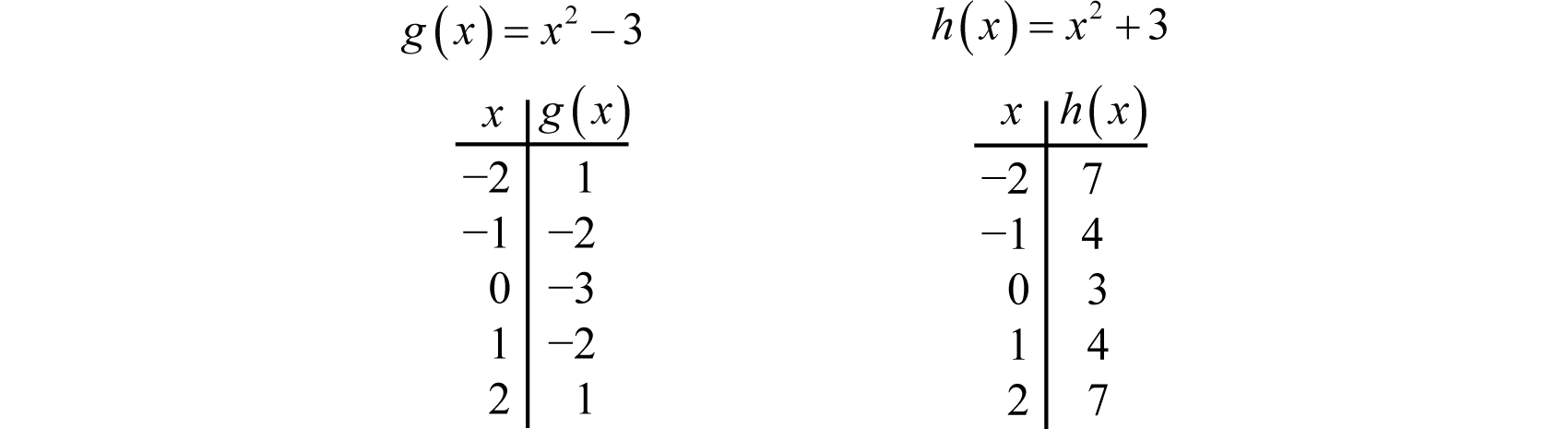 | |
 | 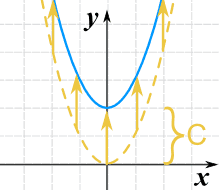 |
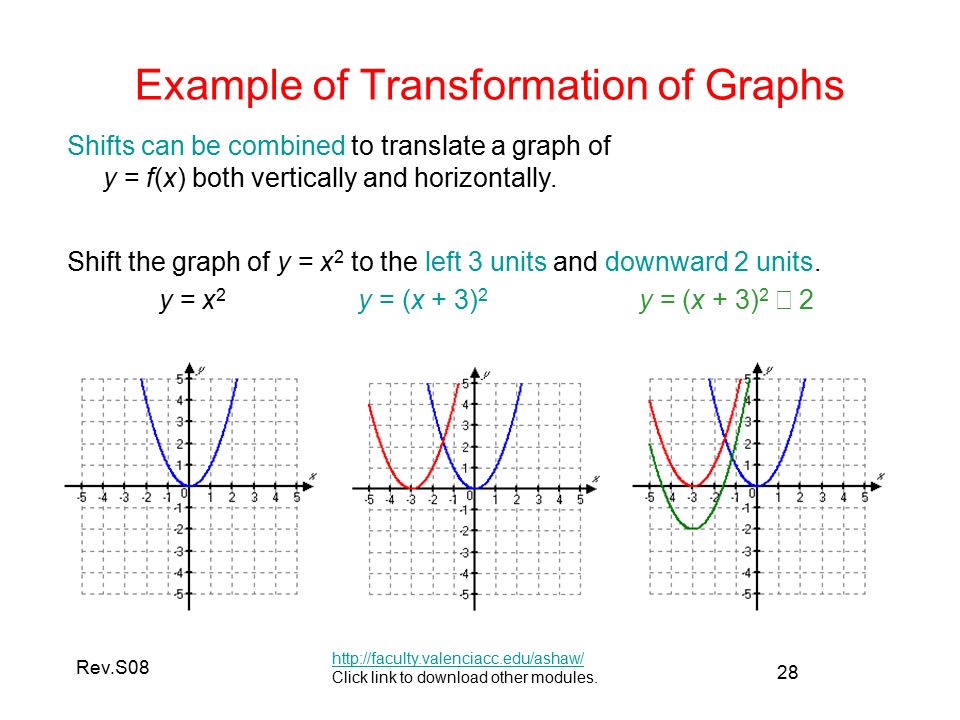
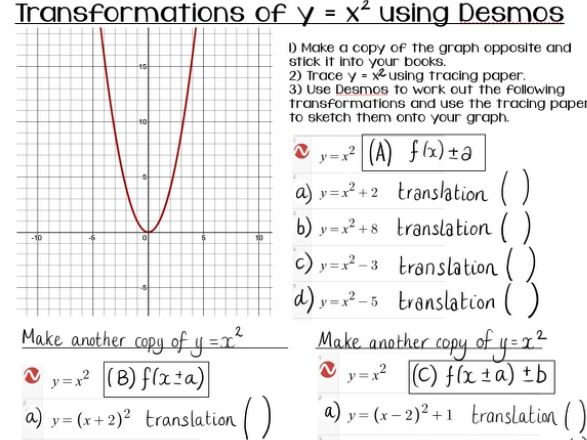
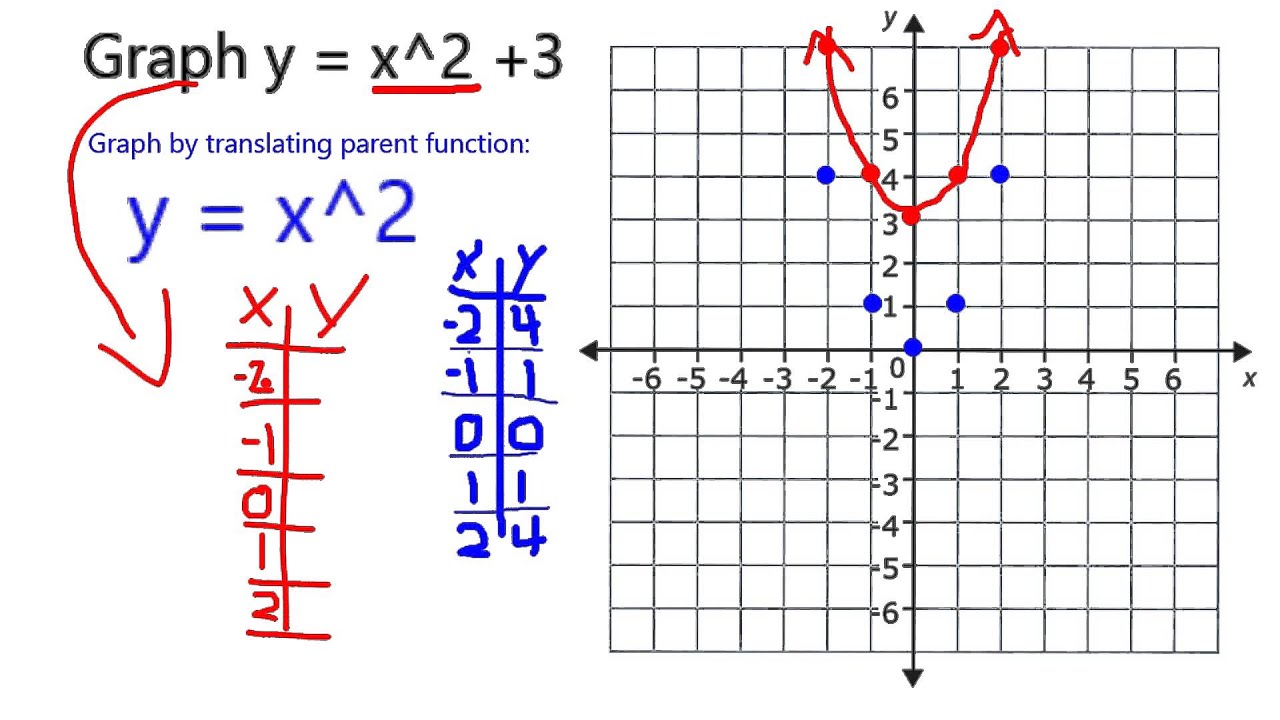
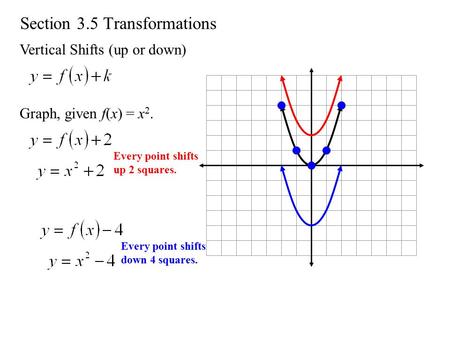
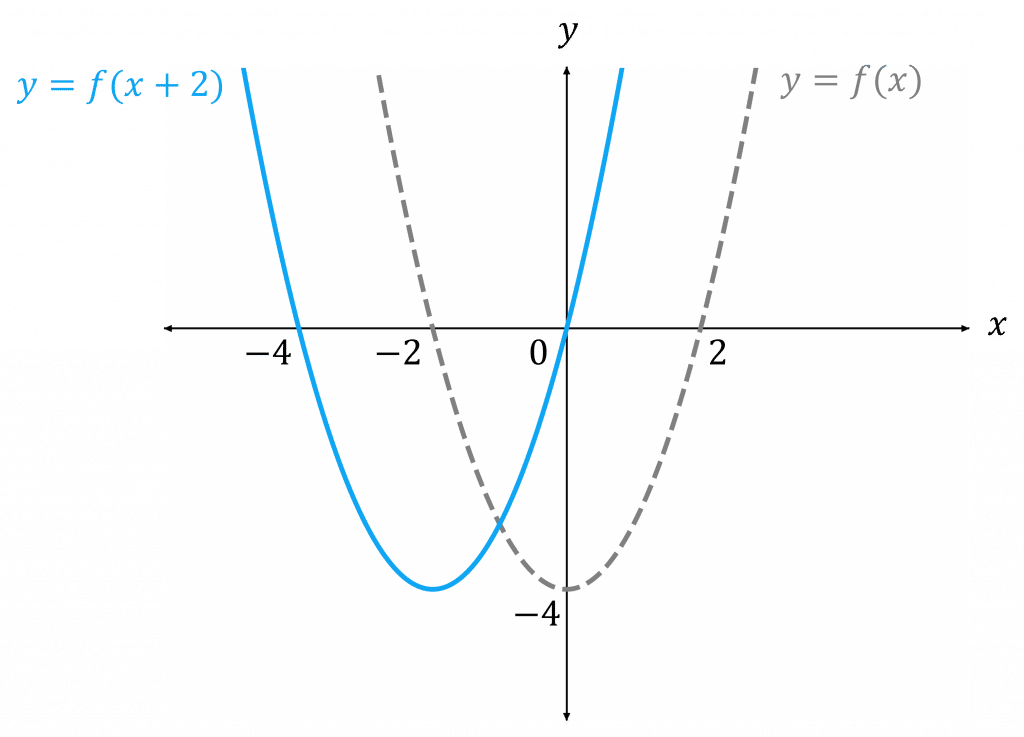
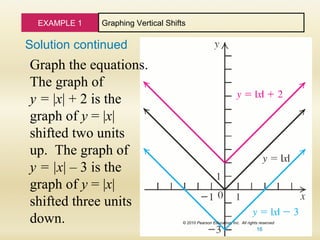
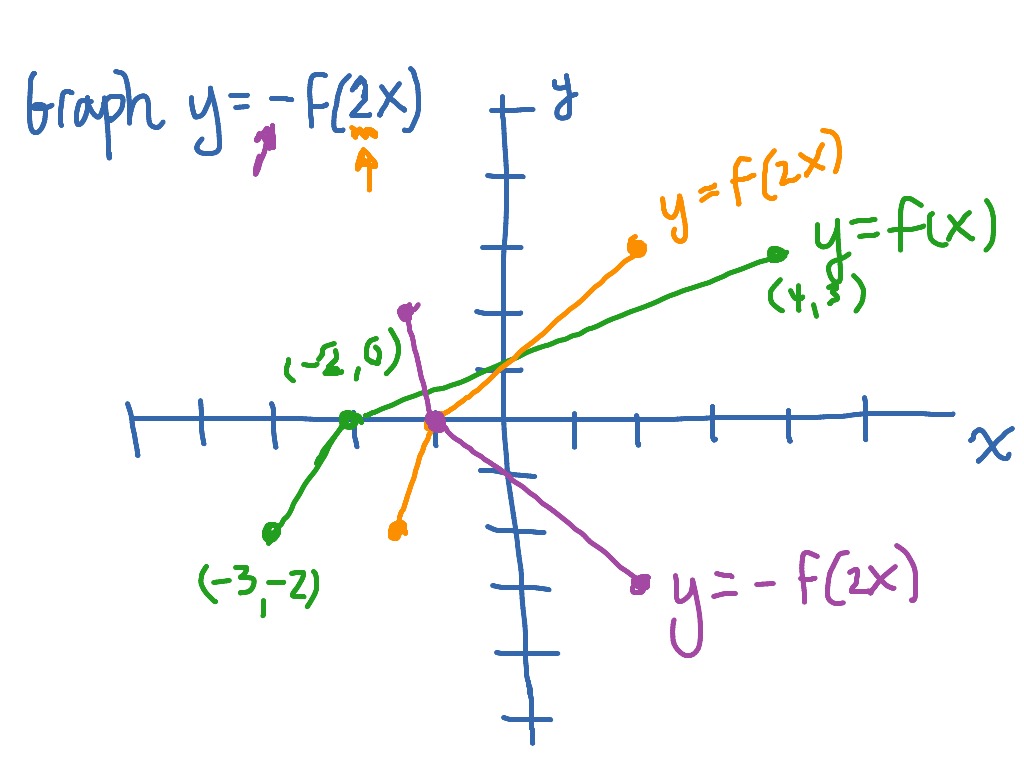
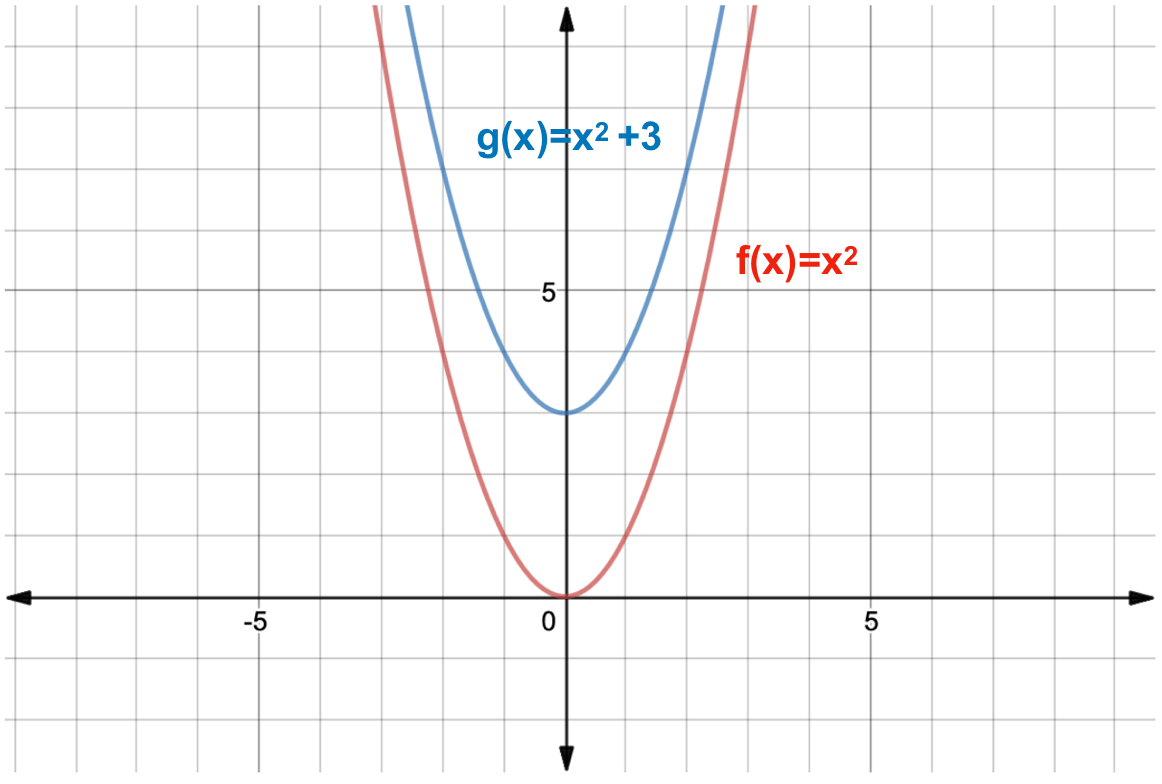
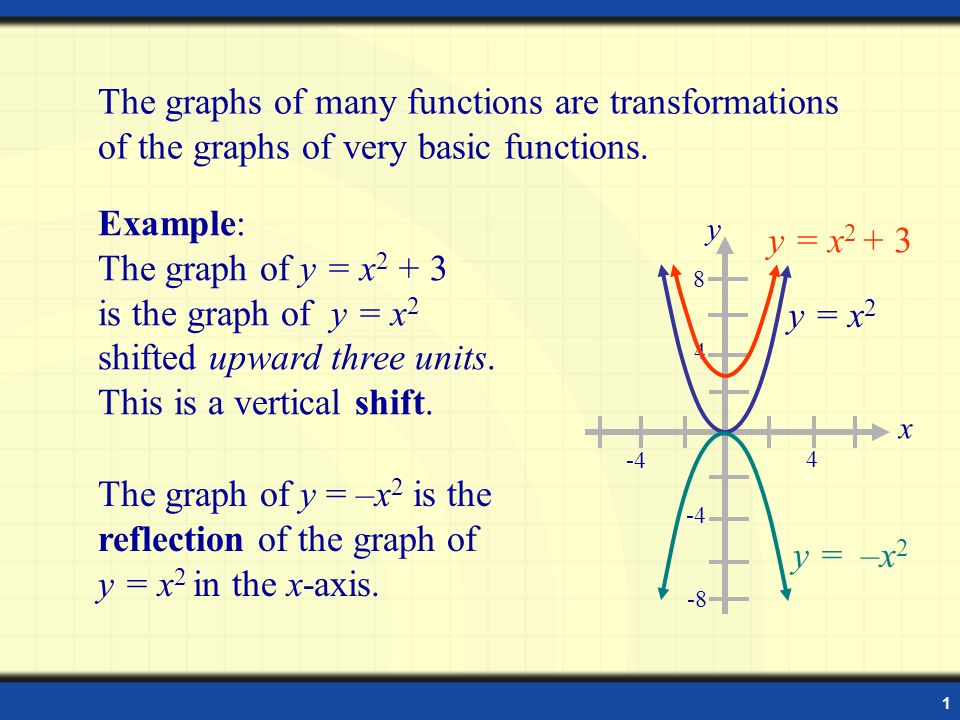
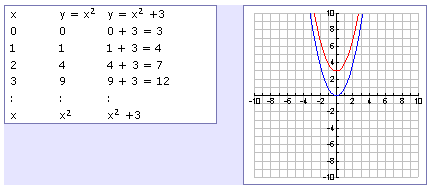
A vertical translation is a rigid transformation that shifts a graph up or down relative to the original graph This occurs when a constant is added to any function If we add a positive constant to each y coordinate, the graph will shift up If we add a negative constant, the graph will shift downThis example uses the basic function \ (y = f (x)\) This can then be uses to draw related functions Notice that the main points on this graph are \ (x = 2,\,1,\,4\) Graph of y = f (x) k
Incoming Term: graph of y=x^2 transformations,




0 件のコメント:
コメントを投稿